Все натуральные числа рождаются из единицы прибавлением ее же самой. И все равноправны. Но умножение (и деление) выделяет из них числа-алмазы (не имеющие множителей).
Это 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 39 и т.д.
Найти закон их распределения - это мечта
математиков уже много веков (вспомним
решето Эратосфена). Этим
занимается теория чисел - наука, не имевшая
никакого практического применения, пока за
нее не взялась криптография.
Пожалуй, самый мощный результат получил еще Леонард Эйлер:
число простых чисел, не превышающих число N, примерно равно числу N / ln( N ).
Я
попробовал исследовать расстояния между
соседними простыми числами, беря все
увеличивающиеся интервалы: простые числа
до тысячи, до десяти тысяч, ..., до миллиарда (ничтожная
доля, ведь они уходят в бесконечность 
). Понятно, что в среднем расстояния растут.
Как сравнивать? А как мы сравниваем
маленькое фото и большой плакат? - Приводим
к единому масштабу. Заодно хотелось бы,
чтобы и лицо было в одном ракурсе. 
Вот и в математической статистике есть
единый масштаб: нулевое среднее и единичная
дисперсия. А ракурс - будем рассматривать
функции распределения.
Здесь
видно, что ступенчатая функция
распределения приближается к гладкой
кривой - стандартному пуассоновскому
распределению. Ради наукообразия в правом
столбце показано, как уменьшается отличие
между двумя кривыми в норме L2 .
Уменьшается, но страшно медленно. 
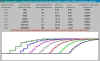
Математика эти графики поражают, не математику представляются курьезными. В чем причина? - Для математика простые числа - абсолютно детерминированный объект, а распределение Пуассона характеризует совокупность случайных независимых процессов. И вот детерминированное и случайное оказываются связанным! Сформулируем гипотезу:
расстояние между соседними простыми числами распределено подобно Пуассоновскому закону.
Являются ли эти графики математическим доказательством - нет.
Каково
это слышать прикладникам? Даже эксперимент,
опирающийся на статистику из 50 миллионов 847
тысяч 534 простых чисел, ничего не доказывает!
Но такова математика бесконечностей.
Даже школьник (но умный) способен указать
место в натуральном ряду, где 50 миллионов
чисел подряд не являются простыми!
Первая мысль - не вытекает ли этот результат из теоремы Эйлера? Вот это единственно, что доказано.
Рассмотрим
квазипростые числа Ni,
определяемые соотношением i = Ni
/ ln( Ni ), i = 3, 4, ... Одной из
характеристик функции распределения
является выпуклость (как у распределения
Пуассона) или вогнутость графика. Так вот,
для квазипростых чисел график будет
вогнутым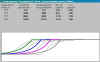 
Это доказывается исследованием 3-й производной функции N( i ) - обратной к функции i = N / ln( N ).
Специфика гипотезы - в том, что она не разбивается на части в отличие от Большой теоремы Ферма (случаи N = 3, 4, ... ).
